DRP | Optimal Control

in Projects

“Direct Reading Program in Mathematics at University of Florida” 

Note: Use a desktop browser to view the interactive table of contents.

Directed Reading Program (DRP) is mentoring initiative designed to give motivated undergraduates an opportunity to explore advanced mathematics topics under the guidance of a graduate stduent mentor.

Click this to learn more about DRP

How to mathematically optimize drug regimens using optimal control

🔬 Kyle Adams, Julia Bruner, Alexandra Haddad, Drew Nelson, Lauren Song, Kayla Adams

Institution: University of Florida

Semester: Spring 2026

Reading Materials

Meetings: Every Tuesday Period 7(1:55-2:45) in LIT 368

Week 1

Reading

  • “Introduction” Section of How to mathematically optimize drug regimens using optimal control, referred to as “main paper.”

  • Guied Questions

    1. Why is optimal control preferred to standard “guess-and-check” methods?
    2. How “good” does a model have to be to apply optimal control to it?
    3. What does QSP stand for? Compare optimal control systems to QSP models.
    4. Take a look at the outline in figure 1. What questions or comments about it can you come up with?

Week 2

Date: January 20th, 2026

  1. Optimal control theory: Optimal control theory is a powerful tool in mathematical optimization that allows us to find control functions that optimize the trajectory of a PDE with respect to some payoff function. There are multiple approaches this theory utilizes to find such a control, from the calculs of variations approach, to the Pontryagin Maximum principle and dynamic programming. Optimal Control Theory

  2. Mechanistic (and semi-mechanistic) model: describe systems (biological in our case) based on known laws/concepts. Semi-mechanistic describe systems based on known laws, but are flexible to mechanisms that aren’t completely understood.

  3. QSP Model: “Quantitative Systems Pharmacology” model: a mathematical model incorporates drug effects.
  4. In silico (and in vitro, in vivo, etc): In sillico = “performed via computer simulation.” In vitro = “performed outside a living organism” (like a petri dish). In vivo = “performed within a living organism”

Here, we discussed comparing HIV Dosing Regimens constant therapy (traditional) and optimal therapy (optimizes treatment)

In HIV, constant therapy is continous drug pressure to suppress viral replication optimal control is time-varying, adaptive dosing that minimizes toxicity, resistance, and cost while maintaining control.

Objective Functionals: an objective functional allows researchers to summarize multiple goals such as maximizing healthy T cells whille minimizing infected cells and drug toxicity into one mathematical expresion to find the best possible treatment plan.

Applications in Disease Treatment:

  • HIV Dosing: simulations show that optimal therapy can lead to better outcomes, such as maintaining higher T cells counts and lower infection levels, even when the total drug exposure (Area Under the Curve) remains the same as traditional methods.

  • Chronic Myeloid Leukemia (CML): a comparison of various drug regimens demonstrates that a constrained optimal regimjen achieves a better value (a lower objective functional score) over five years compared to standard constant-dose regimens.

Week 4

Date: February 3rd, 2026

Artificial Pancreas: A real-world application of control theory (closed-loop insulin delivery) automatically adjust dosage based on real-time glucose monitoring. Algorithms for a Closed-Loop Artificial Pancreas: The Case for Model Predictive Control

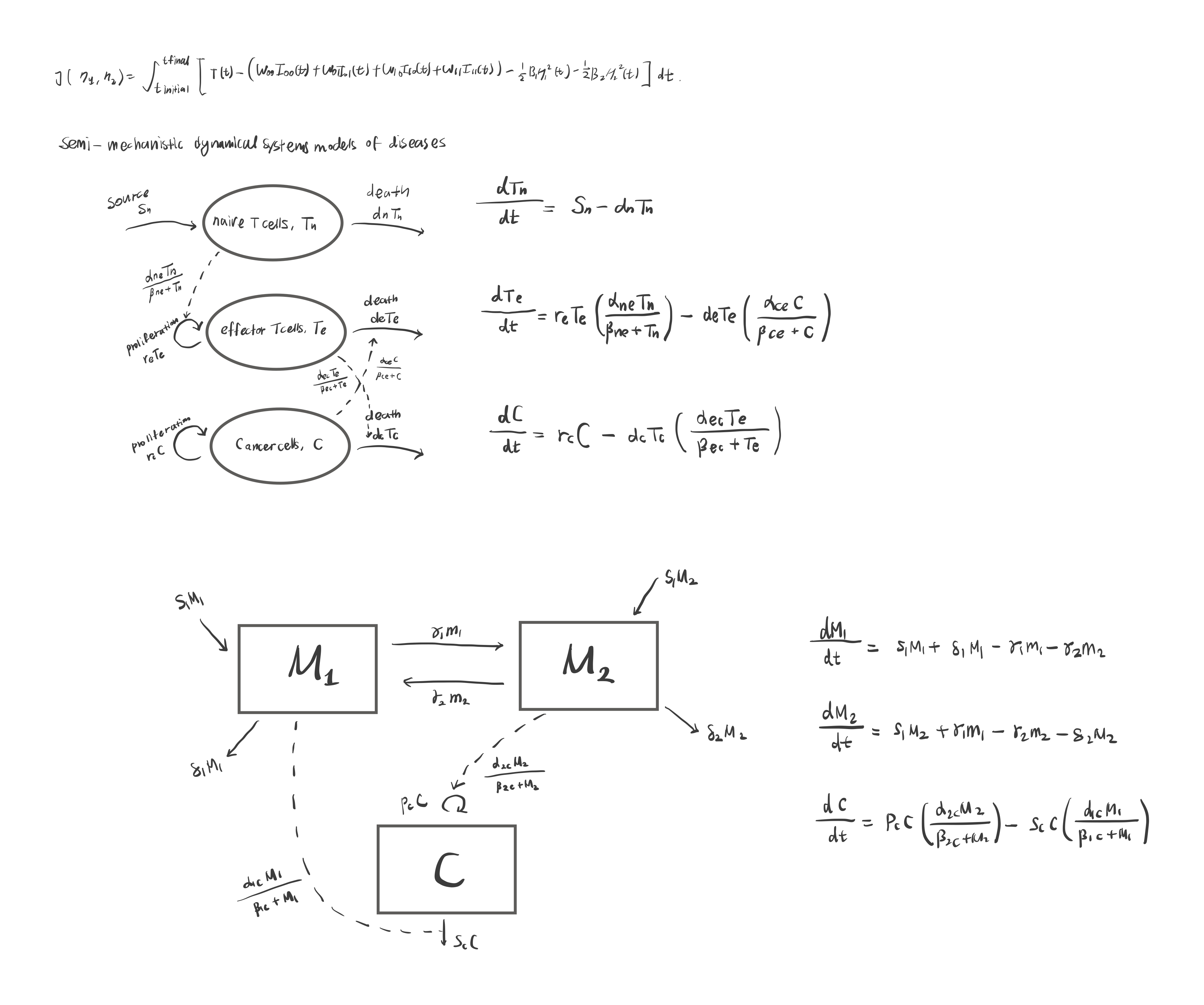
Semi-mechanistic dynamical systems models of diseases

Week 5

Date: Feburary 10th, 2026

Practice drawing a model diagram, given the equations

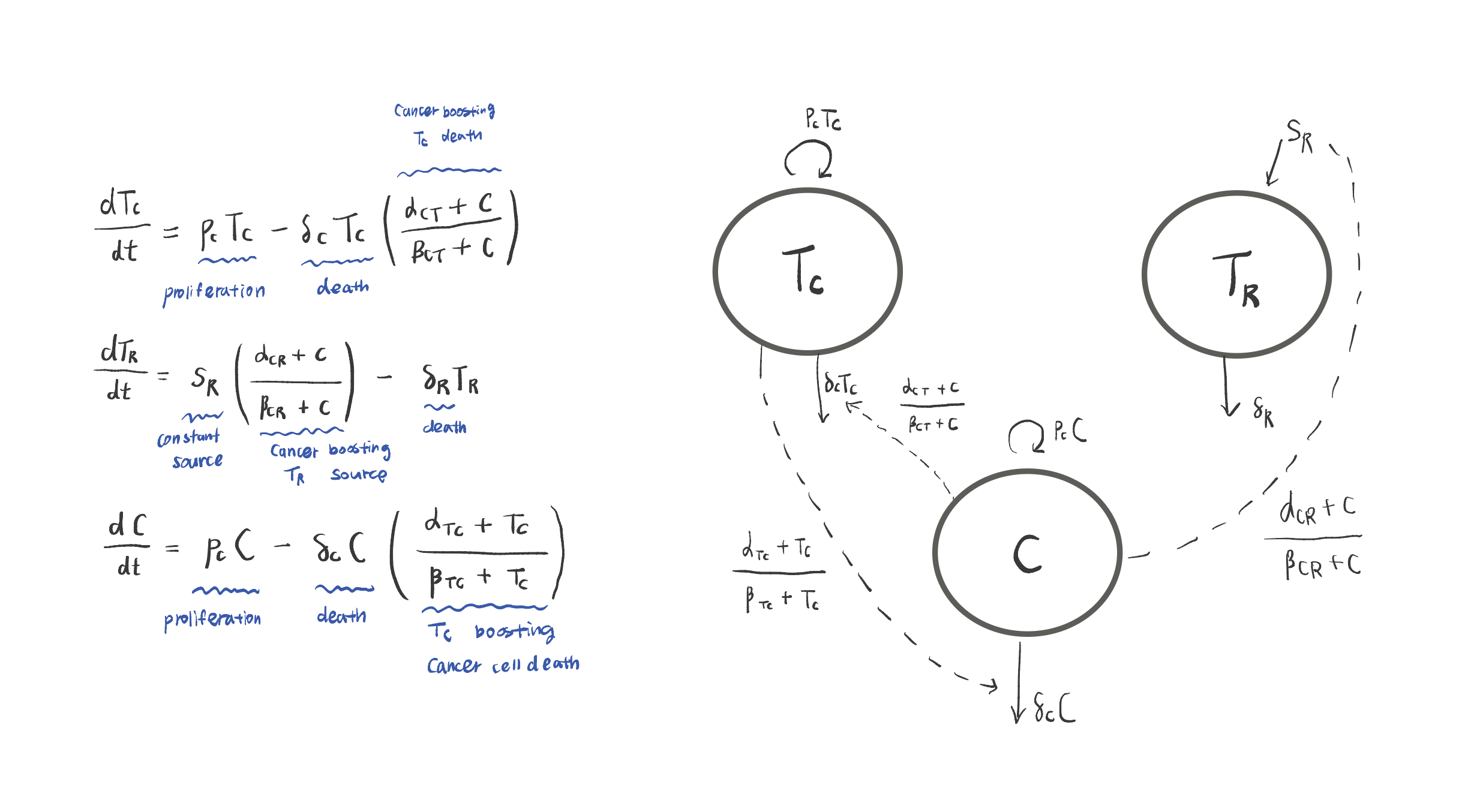
equations to diagram

Ways to model growth

Understanding Immune Dynamics in Liver Transplant Through Mahtematical Modeling

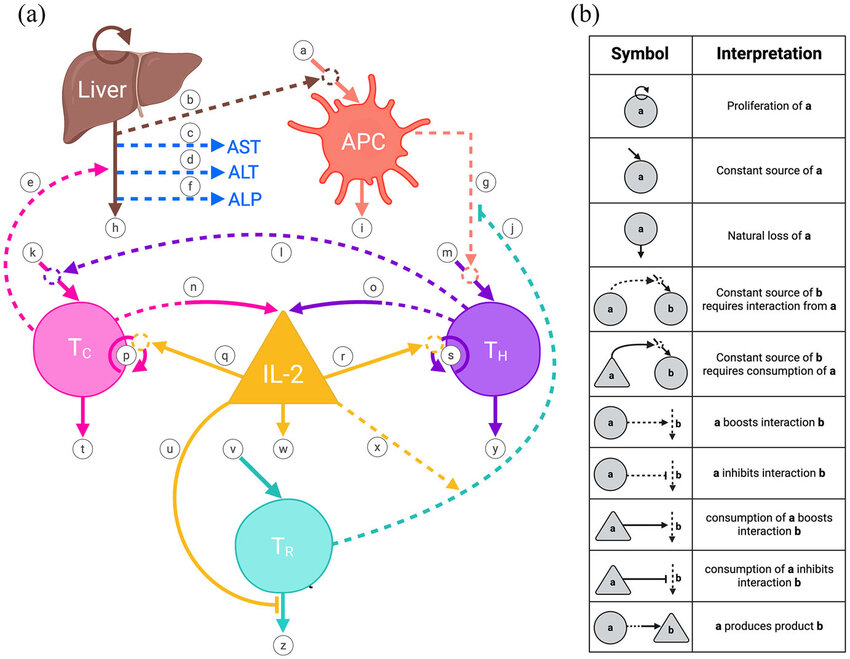
figure 1

This is the model diagram, dynamics of graft rejection in liver transplantation.

Click link to read full article

Equation 4 models